[알고리즘] 위상정렬

위상 정렬

방향 그래프의 정점들을 "선후 관계(의존 관계)"에 따라 나열하는 정렬 방법이다.

단, 위상 정렬은 비순환 방향 그래프(DAG : Directed Acyclic Graph)에서만 가능하다

 

만약 순환이 있다면, 어떤 노드도 “처리 순서를 앞에 둘 수 없기 때문에” 선형 정렬 자체가 불가하다.

(진입 차수가 0이 될수 없는 구간이 존재하고, 그러면 각 정점은 우선순위가 없으며 위상 정렬을 통해 탐색 순서를 정의할 수 없다)

 

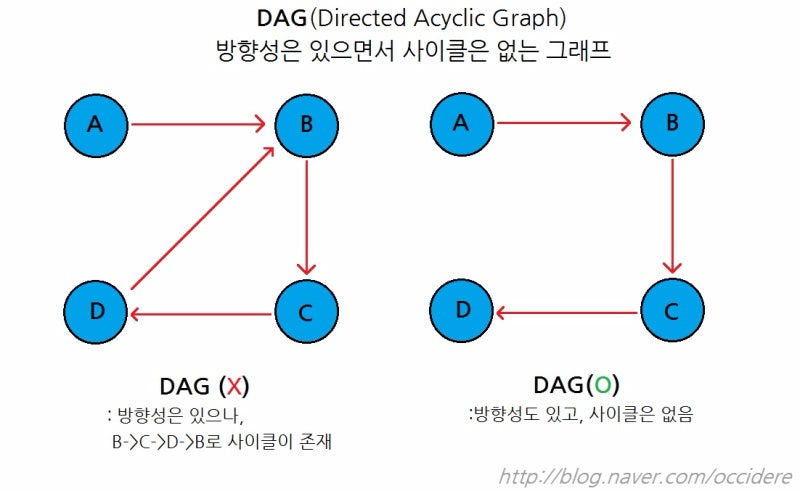
위상 정렬 예시 : 라면 끓이기

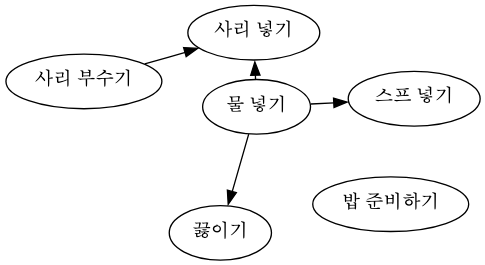
1. DFS 기반 위상 정렬

깊이 먼저 따라가서, 끝에서 역순으로 쌓는다

1. 사리 부수기 → 사리 넣기 → 물넣기
2. 스프넣기 → 물넣기
3. 끓이기 → 물넣기
4. 밥 준비하기 (독립)

✔️ 결과 예시 (역후위 순회) :

밥 준비하기 → 사리 넣기 → 사리 부수기 → 스프 넣기 → 끓이기 → 물 넣기
→ 뒤집으면 →
물 넣기 → 끓이기 → 스프 넣기 → 사리 부수기 → 사리 넣기 → 밥 준비하기

1. BFS 기반 위상정렬

진입 차수가 0인 노드들 부터 시작해서 정렬하면 :

1. 진입 차수 0인 노드 :
   1. 사리 부수기
   2. 물 넣기
   3. 밥 준비하기
2. 그 다음:
   1. 사리 넣기 (사리 부수기 이후)
   2. 끓이기 (물 넣기 이후)
   3. 스프 넣기 (물 넣기 이후)

✔️ 결과 예시 : 선행 조건만 맞으면 순서는 여러가지 가능

사리 부수기 → 물 넣기 → 밥 준비하기 → 끓이기 → 스프 넣기 → 사리 넣기  
or
물 넣기 → 사리 부수기 → 밥 준비하기 → 스프 넣기 → 끓이기 → 사리 넣기

위상 정렬에는 DFS를 이용한 방법과 진입 차수 (Indegree)를 이용한 총 2가지의 방법이 있다.

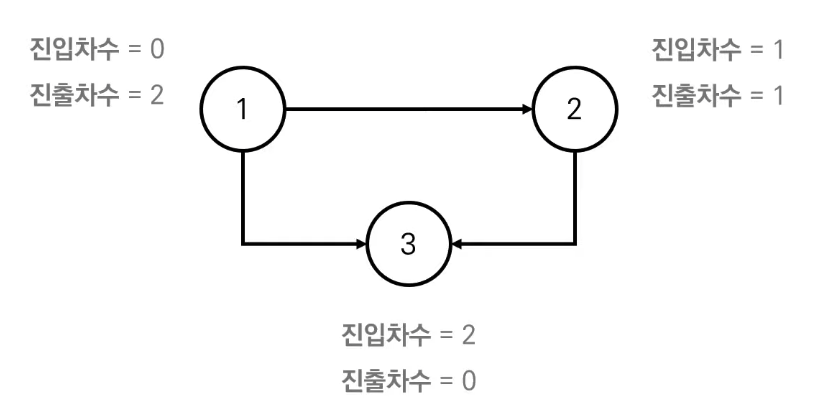
진입 차수 (Indegree) : 특정 노드로 들어오는 간선의 개수

진출 차수 (Outdegree) : 특정 노드에서 나가는 간선의 개수

 

DFS와 위상정렬

위상 정렬은 DFS 종료 순서를 뒤집은 것으로 구할 수 있다.

• DFS에서 한 노드의 모든 자식 노드를 방문한 뒤
• 그 노드를 스택에 push
• 마지막에 스택을 뒤집으면 위상 정렬 결과

단, 이 방식은 역행 간선(back edge)이 없는 DAG에서만 가능. 순환이 있는 경우 DFS 중 back edge로 정렬 실패

큐(BFS)를 이용한 위상 정렬

✅ Kahn’s Algorithm

1. 모든 정점의 진입 차수(in-degree) 계산
2. 진입 차수가 0인 노드를 큐에 넣음
3. 큐에서 꺼내면서 해당 노드와 연결된 간선 제거 → 연결된 노드의 진입 차수 감소
4. 진입 차수가 0이 되면 다시 큐에 삽입
5. 모든 노드를 처리하면 위상 정렬 결과 완성

from collections import deque

def topological_sort(vertices, edges):
    in_degree = [0] * vertices
    graph = [[] for _ in range(vertices)]

    for u, v in edges:
        graph[u].append(v)
        in_degree[v] += 1

    queue = deque([i for i in range(vertices) if in_degree[i] == 0])

    topological_order = []
    while queue:
        node = queue.popleft()
        topological_order.append(node)

        for neighbor in graph[node]:
            in_degree[neighbor] -= 1
            if in_degree[neighbor] == 0:
                queue.append(neighbor)

    if len(topological_order) != vertices:
        return []

    return topological_order

위상 정렬 코드 구현 핵심

공통 개념 요약

• 그래프 구조: graph[from] = [to1, to2, ...]
• 진입 차수 배열: indegree[i] → i번 노드를 향하는 간선 수
• 위상 정렬 결과: topo_order 리스트에 저장

입력을 보고, “ 작업 순서 / 선행 조건 “ 이라는 키워드가 보이면 위상 정렬을 의심해보아야 한다.

import heapq
from collections import deque

graph = [[] for _ in range(N+1)]
# 사용: defaultdict(list) 또는 graph = [[] for _ in range(N+1)]

indegree = [0] * (N+1)

queue = deque()

for i in range(1, N+1):
    if indegree[i] == 0:
        queue.append(i)

큐를 사용하는 위상정렬

from collections import deque

def topo_sort_queue(N, graph, indegree):
    queue = deque()
    topo_order = []

    # 진입 차수 0인 노드 큐에 삽입
    for i in range(1, N + 1):
        if indegree[i] == 0:
            queue.append(i)
        # 큐에서 하나씩 꺼내서 결과에 추가
    while queue:
        node = queue.popleft()
        topo_order.append(node)
                # 꺼낸 노드와 연결된 다음 노드들의 진입 차수를 1씩 줄임
        for next in graph[node]:
            indegree[next] -= 1
            # 진입 차수가 0이 되면 다시 큐에 추가
            if indegree[next] == 0:
                queue.append(next)

    return topo_order

🟡 이 방식은 순서가 여러 개 존재할 수 있음. 정해진 순서가 중요하지 않은 위상 정렬 문제에 적합.

heapq 를 이용한 위상 정렬

import heapq

def topo_sort_heapq(N, graph, indegree):
    heap = []
    topo_order = []

    # 진입 차수 0인 노드 우선순위 큐에 삽입
    for i in range(1, N + 1):
        if indegree[i] == 0:
            heapq.heappush(heap, i)

    while heap:
        node = heapq.heappop(heap)
        topo_order.append(node)

        for next in graph[node]:
            indegree[next] -= 1
            if indegree[next] == 0:
                heapq.heappush(heap, next)

    return topo_order

🟢 이 방식은 번호가 작은 노드부터 우선 탐색하고 싶을 때 사용. 정렬된 결과가 필요할 때 사용

위상 정렬 + DP

from collections import deque

N = ...  # 노드 수
graph = [[] for _ in range(N+1)]
indegree = [0] * (N+1)
time = [0] * (N+1)    # 각 노드 작업 시간
dp = [0] * (N+1)      # 각 노드까지 걸리는 누적 시간

# 그래프 구성 및 진입 차수 설정
for i in range(1, N+1):
    time[i] = 작업 시간
    for 선행노드 in 입력:
        graph[선행노드].append(i)
        indegree[i] += 1

# 진입 차수 0인 노드부터 시작
queue = deque()
for i in range(1, N+1):
    if indegree[i] == 0:
        queue.append(i)
        dp[i] = time[i]  # 자기 자신만 걸리는 시간

while queue:
    node = queue.popleft()
    for next in graph[node]:
        # 이전 노드까지의 누적 시간 중 최대값을 이용
        dp[next] = max(dp[next], dp[node] + time[next])
        indegree[next] -= 1
        if indegree[next] == 0:
            queue.append(next)

# 결과: dp[1] ~ dp[N]에 각 노드까지의 최소(또는 최대) 시간 저장됨

🔵 이 방식은 이전 노드의 결과값을 바탕으로 현재 노드의 최적값을 갱신해야 할 때 사용. 

→ 어떤 작업이 완료되기까지 걸리는 최소 시간이나 최대 비용을 구하는 문제인 경우